Structures and Processes of a Galois Connection
Written by @prathyvsh | Version 0.08
A look at Galois connection in the context of binary relations between two sets. The post unfolds its local constituent structures and processes. It then folds these up, to highlight the global picture of the interesting dualities in action.
Index
Introduction
- The Theatre of Galois Connection A Bird’s Eye Diagrammatic View
- The Two Tales Two Ways to Read the Central Idea
- On Navigation Cues for Reading
- The Storyboard Card Deck of the Cast and Crew
Constructing the Concept Lattice
- Structural Interpretation
- Process Interpretation
- A Note on the Terminology
Unwinding the Concept Lattice to a Context
- Unwinding the lattice
- Atlas of Contexts
- Birkhoff Representation Theorem
The Mirror of Duality
- Inside/Outside
- Duality of the Powerset
- Structure vs. Process
- Polarity vs. Axiality
History
- Philosophy
- Mathematics
- Interpollination
Prior Art and Future Work
Lexicon
Bibliography
Introduction
This post is a conceptual overview of Galois connection. It is a general idea that makes its appearance throughout mathematics. It was historically uncovered from the context of solvability of the quintic (fifth degree) equation. But since then, mathematicians started spotting it in many guises in varied contexts especially with the rise of mathematical structures. I use the context of relation between sets to illustrate the structures and processes of this concept as it makes the idea easy to grasp.
The post makes minimal use of equations and computations so that I can give a bird’s eye conceptual view of the landscape. A frog’s eye view post will shortly be published where I get into the nitty-gritty proofs and computations.
It is written as an exposition of Galois connection maximally using diagrams to communicate the ideas here. Someone curious enough to reason about the structures using the visuals will gain some intuition into the structures and processes at work here. But it is indeed true that a fuller absorption of the content here will require some mathematical maturity as the article assumes a basic mathematical background in sets, relations, partial orders, and lattices. I hope to augment this with an interactive environment and animations in a future revision of this article and provide the supplementary materials that enable a novice towards comprehending all of the necessary background. But for now, this is my first step towards elucidating the beautiful interactions between Galois connections and concept lattices.
My hope is that by depicting the internal and external structures and processes at play here, it will enable people who haven’t seen this before to visually reason and understand the structures and process at play here. I hope that by maximally visualizing the internal and external details, even ones familiar with the construction/deconstruction of Galois lattices will find something worthy of appreciation.
Introduction
The Theatre of Galois Connection
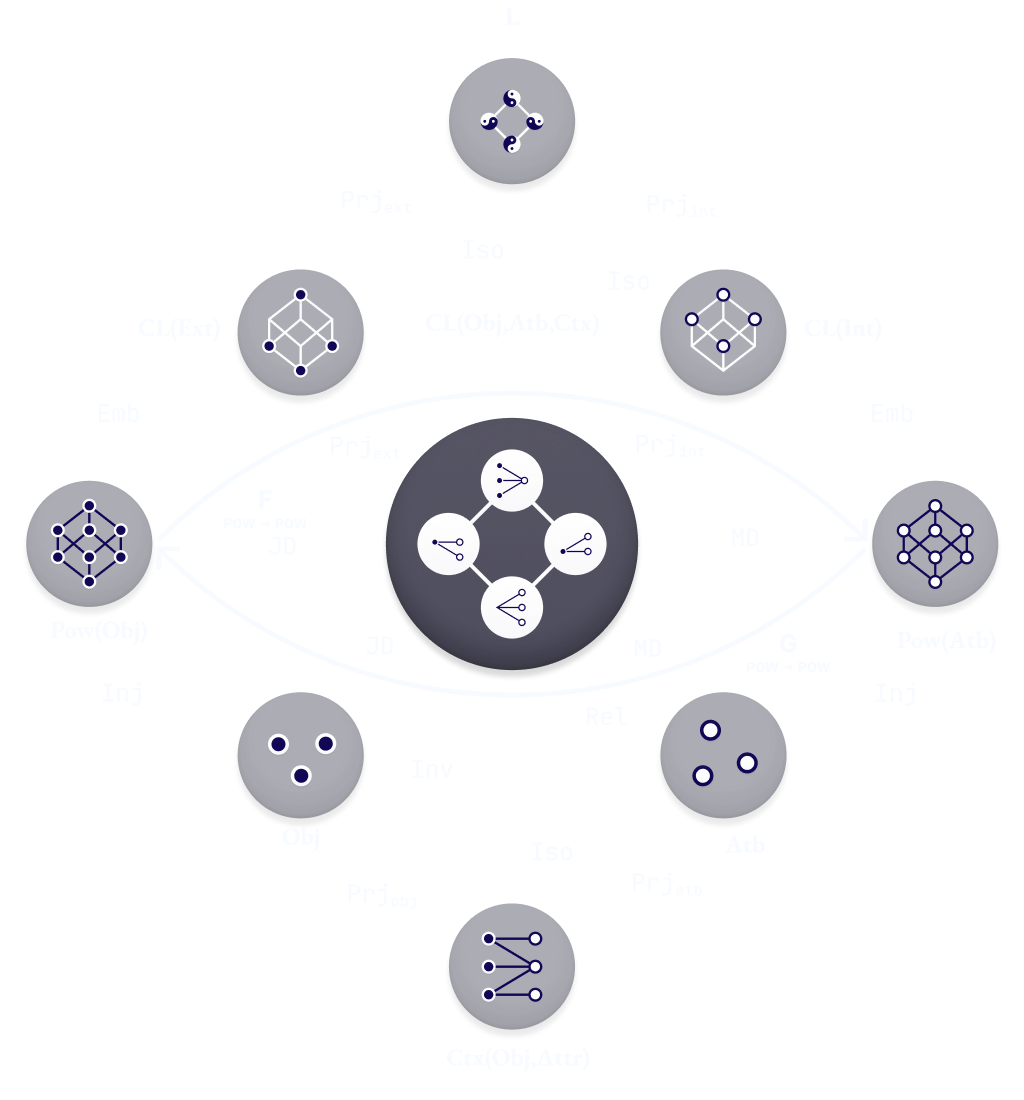
A Bird’s Eye Diagrammatic ViewWe will take a look at how a concept lattice can be constructed from a given context between two sets, and how it conversely can be unwound so that a context can be obtained from any concept lattice. Towards this purpose, let us first get acquainted with a map of the various acts that are happening between the “cast and crew” of entities involved in the Galois connection that generates a concept lattice from a given relation. We will call it the Eye of Galois. It will aid us in getting a comprehensive view of the different objects/maps involved in the idea. At the end of this article, I will reveal a lexicon where you can learn about each of the ideas in detail.
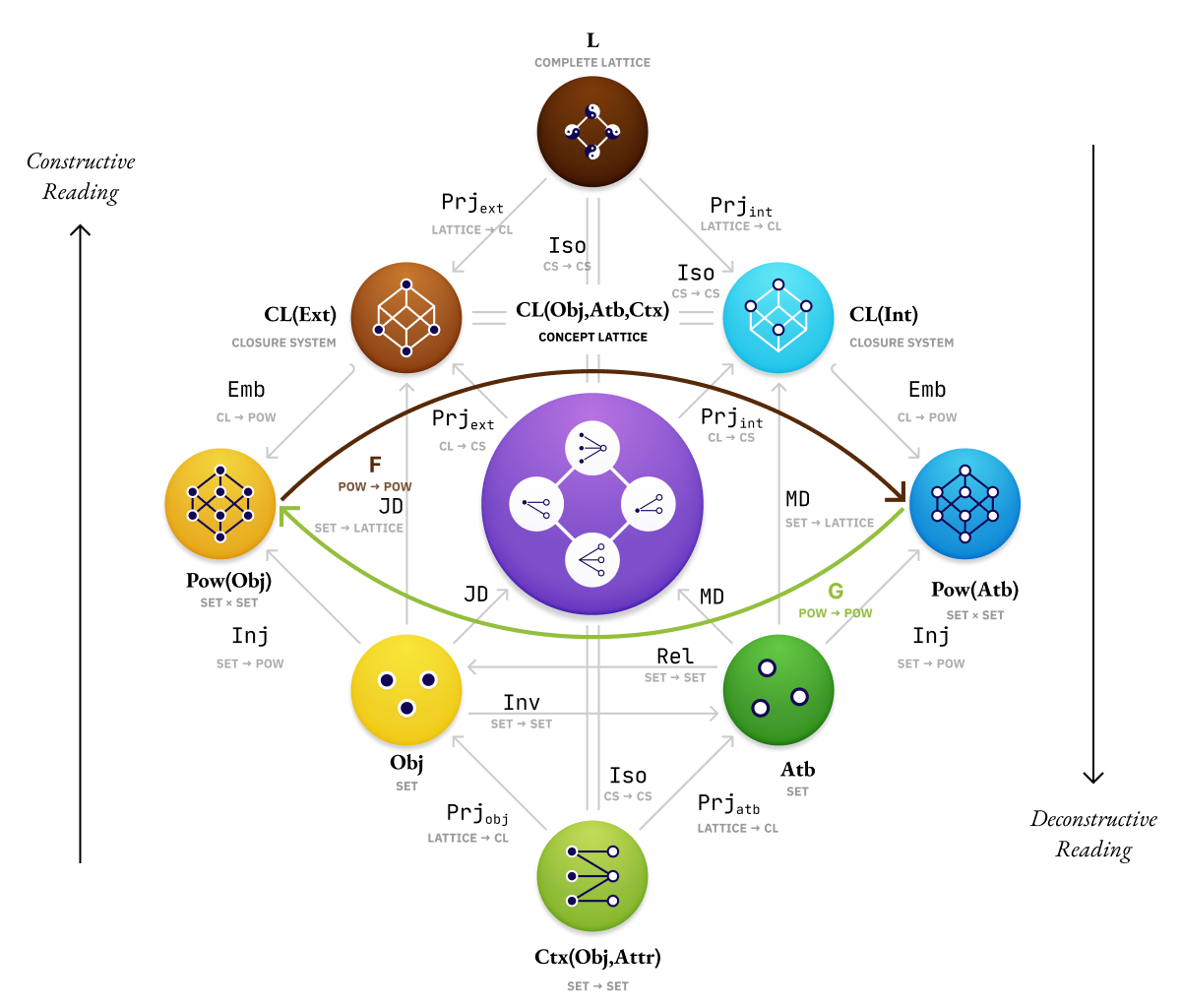
This diagram captures the central structures and processes at play. But it is a rather cryptic diagram. Let us start making this a juicy framework by slowly unfolding the structures and processes behind the curtains. We will develop our intuition on the various objects and relations it consists of. Each of the circle shows the main mathematical object and the arrows between them depict the interconnections it has with other objects.
Introduction
The Two Tales
Two ways to read the central ideaThere are two ways to read this diagram as to 1/ how it folds up to and 2/ unfolds down from this concept lattice in the nucleus of the diagram:
CL(Obj, Atb, Ctx)Concept Lattice
These ways of readings can respectively be thought of as 1/ construction and 2/ deconstruction of the concept lattice. The construction takes a context and builds up a complete lattice from it. In the deconstruction, we unwind the complete lattice to get back a context. These two readings can be visually emphasized by swapping the context and concept lattice as the source and target.
Construction
Context → Concepts as Complete Lattice
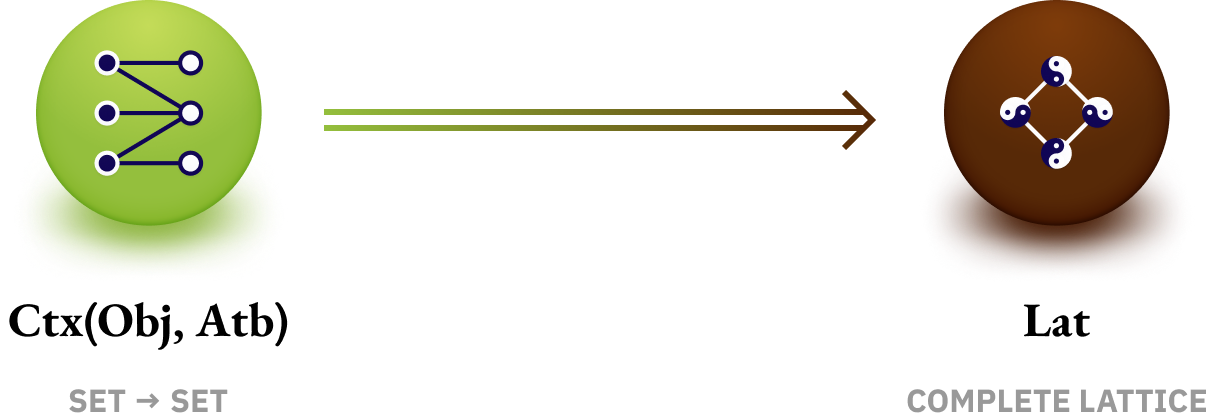
Construction of concepts CL(Obj, Atb, Ctx) from the context Ctx(Obj, Atb) between objects Obj and Atb. The concepts so obtained are structured as a complete lattice Lat.
Deconstruction
Complete Lattice as Concepts → Context
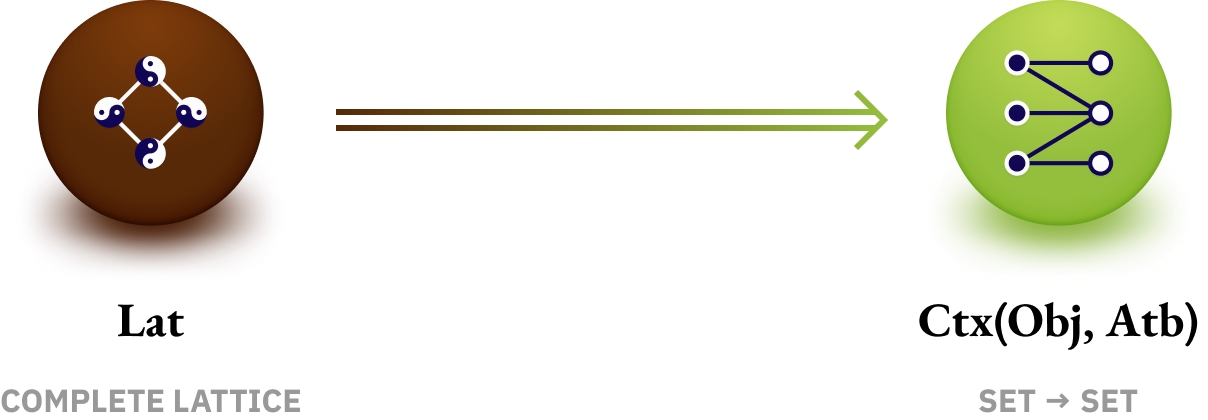
Deconstruction of a complete lattice Lat by regarding it as a concept lattice CL(Obj, Atb, Ctx), we can encode any complete lattice as a context Ctx(Obj, Atb) relating two sets Obj and Atb.
These two directions of readings are two central ways through which we derive practical applications from this theory of Galois connection in the context of relations. We will examine these two “modes” closely in the upcoming sections.
Introduction
On Navigation
Cues for ReadingIn unbundling the concert among various objects and maps, we will employ a miniature version of this diagram. Different parts of this diagram will be highlighted as per the emphasis laid on in a given section.
For example, here are a few configurations of the miniature diagram which highlights what concepts are emphasized in a particular section.
Context, Objects and Attributes, and their Powersets
Concept Lattice and Galois connection between Powersets
Isomorphism between complete lattice and context via concepts
With that book keeping details out of the way, let us dive right in and examine the Galois Connection.
Introduction
The Storyboard
Card Deck of the Cast and Crew
The Context
We start with a context composed of relations between two sets. This can be represented as a bipartite graph connecting a domain and a codomain.
Quotients & Kernels
We now move to a higher order setting of families of sets when identifying the kernels of the domain and cokernels of the codomain of the context.
A New Basis
Kernels and cokernels embed into their powerset which has the nature of being both a set of sets and a partially ordered lattice. This is where we start to witness the intension/extension duality.
Galois Connection of Powersets
This locates a Galois connection between the powersets. This leads us to understand certain maps as being symmetric between domain and codomain, which mark out what we call a “formal concept”.
Concepts as fixed points
Concepts act as fixed points of the Galois connection. The objects covered by the concept can be thought of as its extent, and the attributes possessed by it as its intent. Every context can be compactly represented by a concept lattice.
Complete lattices as concept lattices
Every complete lattice arises as a concept lattice of join and meet dense maps. CL(Obj) and CL(Atb) are closure systems.
Dense Maps
The maps from objects and attributes to the complete lattice are respectively join dense and meet dense, and they encode the relation Ctx(Obj, Atb).
Complete Result
That completes the result: We have a three-way relationship between concepts, which are complete lattices, that encode a context by virtue of the Galois connection between powersets of objects and attributes.
Stay tuned to read the upcoming chapters!